河内塔与递归

河内塔，又叫汉诺塔，是法国数学家爱德华·卢卡斯于1883年发明，给定一个由八个圆盘组成的塔，这些圆盘按照大小递减的方式在三根桩柱上，需要把整个塔一道另一根桩柱上，一次只能移动一个圆盘，并且必须保证较大的圆盘永远在下面。在电影《猩球崛起》中有这样一个片段，凯撒的妈妈美瞳(Bright eyes)在实验室内在服用一种药物后，智商堪比人类，在对她进行河内塔游戏的测试中，有非常优秀的表现。

河内塔还有一个美丽的传说：有64个这样的圆盘组成的塔，上帝命令一群牧师夜以继日的工作，当牧师完成上面的任务时，塔将坍塌，世界也将毁灭。

我们不防把这个问题再扩大一下，如果有n个圆盘，需要多少次移动才能把塔从一个桩柱移动到另外一个上面？假设一个函数f(x)表示移动x个圆盘所需要的次数，则移动n个需要f(n)次。
再来考虑最大圆盘的情况，当最大的一个圆盘被放到另外的一个桩柱时，必须满足这样一种情况，另外(n-1)个圆盘必须是从小到大依次排列的，如图:

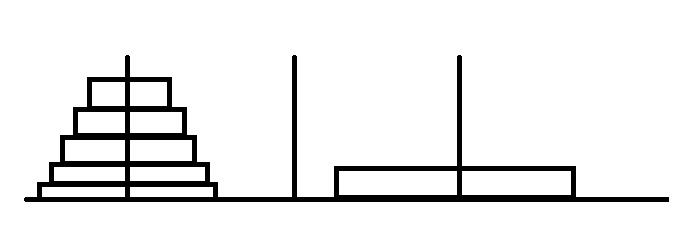
所以我们可以把这个问题分成两个步骤:
1,把n-1个盘子移动到另外一根柱子上
2,把最大的那个盘子放到目标柱子上
这一步需要的移动次数是f(n-1)+1。这时候，我们知道总的需要移动的次数:
f(n) = 2f(n-1)+1
因为接下来还剩n-1个盘子，n-1个盘子移动需要的次数是f(n-1), 我们又知道如果只有1个盘子，它需要的移动次数是1,即:
f(1) = 1
这时候，如果你接触过递归，我相信你已经能写出处理这个问题的函数了:

def move_count(n):
    if n == 1:
        return 1
    else:
        return 2*move_count(n-1)+1

所以我们可以计算出移动3个盘子需要7此，而移动64个盘子18446744073709551615次，如果一秒钟移动10次(这已经是非常快的速度了)，则移动完64个盘子需要的时候为584.94241735亿年，我们知道太阳系的寿命大约为100亿年，目前太阳为50亿岁，也就是说没等这64个盘子移动完，太阳系就已经不复存在了。64个盘子的问题，竟然需要接近6个太阳寿命的时间才能解决，我们不得不感叹人类在时间面前是多么的渺小，所以抓紧时间学习吧，骚年。

回到刚刚这个5行代码可以解决的问题，似乎还没有弄情况怎么回事，假设我们没有学过递归，你上学时一定见过这样的数学题:
已知 f(x) = 2f(x-1)+1,f(1) = 1, 求f(10)
如果你数学不好，肯定这样计算过:
f(1) = 1 , f(2) = 2*1 + 1 = 3, f(3) = 2 * 3 + 1 = 7 … f(10) = 2 * 511 + 1 + 1023
这样解法计算小值还可以，如果计算大值花费的时间就太长了。数学方面，我们可以这样解决:
已知:
f(1) = 1
f(n) = 2*f(n-1)+1
得出:
f(n)+1 = 2*(f(n-1) + 1)
令:U(n) = f(n)+1
则:U(n-1) = f(n-1) + 1
f(n-1) = U(n-1) -1
U(n) = 2*((U(n-1)-1)+1)
U(n) = 2U(n-1)
U(1) = 2
得出:U(n)=2^n
则:f(n) = 2^n -1
另外，如果你是比较善于归纳的人，也可以用数学归纳法推测f(n)=2^n-1,然后予以证明。

递归

汉诺塔问题是一个典型的递归问题，它的特征是知道两个相邻元素的关系和某个边界，求某个固定的值，如求自然数的阶乘:
已知，p(1)=1,p(n)=n*p(n-1)，求p(10)的值，在程序中用递归的思路很好解决:

#include <stdio.h>
    long factorial_recursion(int n){
        if(n==1){
            return 1;
        }else{
            return n * factorial_recursion(n-1);
        }
    }
    int main(int argc,char ** argv){
        int N = 10;
        long fac =  factorial_recursion(N);
        printf("Factorial is is %ld!",fac);
        return 0;
    }

编译这个程序之后，用gdb工具分析:

(gdb) b 6
Breakpoint 1 at 0x4013f3: file fac.c, line 6.
(gdb) r
Starting program: C:\Users\cheng\Desktop/a.exe
[New Thread 1032.0x1688]

Breakpoint 1, factorial_recursion (n=10) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb) n

Breakpoint 1, factorial_recursion (n=9) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=8) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=7) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=6) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=5) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=4) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=3) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb)

Breakpoint 1, factorial_recursion (n=2) at fac.c:6
6               return n * factorial_recursion(n-1);
(gdb) bt
#0  factorial_recursion (n=2) at fac.c:6
#1  0x00401401 in factorial_recursion (n=3) at fac.c:6
#2  0x00401401 in factorial_recursion (n=4) at fac.c:6
#3  0x00401401 in factorial_recursion (n=5) at fac.c:6
#4  0x00401401 in factorial_recursion (n=6) at fac.c:6
#5  0x00401401 in factorial_recursion (n=7) at fac.c:6
#6  0x00401401 in factorial_recursion (n=8) at fac.c:6
#7  0x00401401 in factorial_recursion (n=9) at fac.c:6
#8  0x00401401 in factorial_recursion (n=10) at fac.c:6
#9  0x00401429 in main (argc=1, argv=0x372a00) at fac.c:11
(gdb) n
8       }
(gdb) n
8       }
(gdb) bt
#0  factorial_recursion (n=3) at fac.c:8
#1  0x00401401 in factorial_recursion (n=4) at fac.c:6
#2  0x00401401 in factorial_recursion (n=5) at fac.c:6
#3  0x00401401 in factorial_recursion (n=6) at fac.c:6
#4  0x00401401 in factorial_recursion (n=7) at fac.c:6
#5  0x00401401 in factorial_recursion (n=8) at fac.c:6
#6  0x00401401 in factorial_recursion (n=9) at fac.c:6
#7  0x00401401 in factorial_recursion (n=10) at fac.c:6
#8  0x00401429 in main (argc=1, argv=0x7b2a00) at fac.c:11
(gdb) n
8       }
(gdb) bt
#0  factorial_recursion (n=4) at fac.c:8
#1  0x00401401 in factorial_recursion (n=5) at fac.c:6
#2  0x00401401 in factorial_recursion (n=6) at fac.c:6
#3  0x00401401 in factorial_recursion (n=7) at fac.c:6
#4  0x00401401 in factorial_recursion (n=8) at fac.c:6
#5  0x00401401 in factorial_recursion (n=9) at fac.c:6
#6  0x00401401 in factorial_recursion (n=10) at fac.c:6
#7  0x00401429 in main (argc=1, argv=0x7b2a00) at fac.c:11

上面的中#0-#7称之为一个栈帧，保存着未运行完的函数的局部变量和返回地址，关于程序运行中栈帧的结构请看下图:

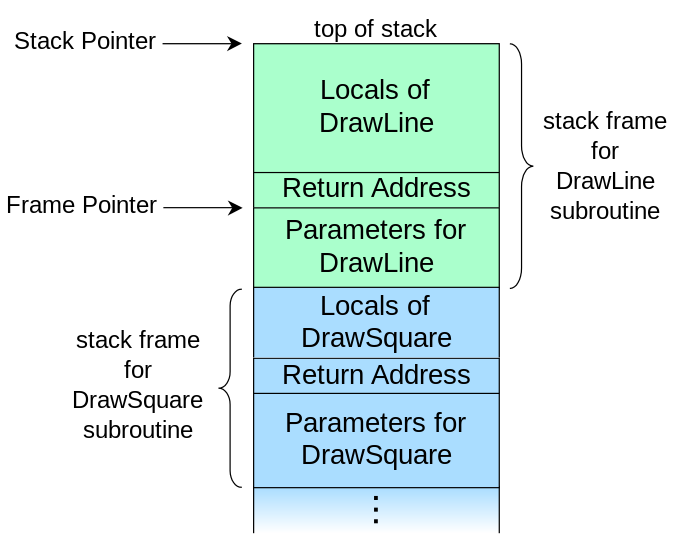
可以看到整个递归的调用实际是函数压栈和出栈的过程，每一次当程序运行到一个函数的时候，则把这个函数压入栈区，如果运行完毕，则反向出栈。

河内塔的移动步骤

我们把河内塔的问题再深入一些，要求程序中打印出具体的移动步骤

#include <stdio.h>
void move_tower(int n,char a, char b ,char c){
    if(n > 0 ){
        move_tower(n-1,a,c,b);
        printf("Move %d  %c -> %c\n",n,a,b);
        move_tower(n-1,c,b,a);
    }
}
int main(int argc,char ** argv){
    char pa = 'a';
    char pb = 'b';
    char pc = 'c';
    move_tower(3,pa,pb,pc);
    return 0;
}

参考资料

1. Call stack