浮点运算，浮点数与定点数(一)

我们评测CPU性能的时候，经常会说道一个概念：浮点运算，我经常在想，浮点运算到底是一个什么样的东西，用得着把它当成评测CPU性能的关键点吗？搞清楚这个问题，首先要说到浮点数和定点数，先看一个例子，用javascript执行console.log(0.1+0.2), 查看其输出，发现0.1+0.2≠0.3!，为什么会这样?这简直太反常识了!

计算机中数字的表示

我们知道，计算机中通过内存存储数据，一个字节有8个位，可以最大表示256个数据，如果用来表示数字，则一个字节可以用来表示0-255，我们可以通过用多个字节来表示更大的数字，如32位计算机中，我们可以直接在CPU中表示和计算最大32位整数，如果大于32位，还可以通过分步的方式进行。但即使是这样，我们还是遇到了一些问题，如果引入非整数，我们发现很多数字根本就无法全部表示，整数之间都有无穷多个数，还有一些无理数，圆周率π，√2等，也是无法进行精确表示的，所以我们在计算机中我们采用近似的方法对其进行表示。

计算机中所有的信息都是用二进制表示的，例如字符“A”，用ASCII码表示其二进制为01000001；整数10，用二进制表示是00001010。那么如果是小数，例如0.2，用二进制如何表示呢？我们知道，10进制的0.1=1/10，二进制的0.1b=1/2，那么我们会发现一个问题，那就是10进制的0.2用二进制表示，尾数是循环的!即:
(0.2)₁₀ = (0.001100110011001100110011)₂

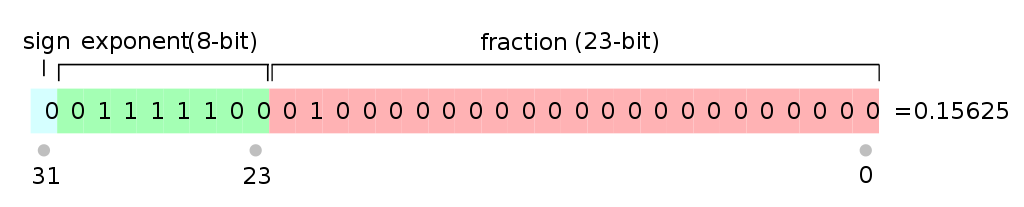
又回到上面的问题，对于这些无法用固定位表示的数，就只能通过近似的方法对其进行表示，所以就会出现文章开头的那个问题。那么我们再深入分析一下，计算机中浮点数到底是如何表示的呢？现代计算机对浮点数的表述遵守IEEE754的标准，包括单精度和双精度浮点数，分别占到32bit和64bit。浮点数的存储包括三个部分，第一部分是符号，占1bit,第二部分是指数位，单精度占8bit，双精度占11bit,第三部分是底数位，单精度占23bit，双精度占52bit，其中符号位1表示负，0表示正，指数位采用阶码的形式。
如0.75用单精度存储:
(0.75)_{10=(0.11)2=(1.1*2^-1)2=(00111111010000000000000000000000)2=0x3f400000=1061158912
我们来验证一下:}

#include <stdio.h>
typedef union{
     int a;   
     float b;
}data;
int main()
{
data d;
d.a=1061158912;
printf("Convert to hex %x\n",d.a);
printf("Convert to float %f\n",d.b);
return 0;
}

用gcc编译运行，打印结果如下:
Convert a to hex 3f400000
Convert a to float 0.750000
浮点数在计算中是以科学计数法表示的，其中需要注意的是底数中，个位数永远都是1，所以编码中不用指出，第二点是单精度浮点数阶码是在指数的基础上加上127形成的，所以在处理的时候需要注意。

浮点数的运算

既然浮点运算成为衡量CPU性能的一个关键指标，那么CPU对浮点数是如何进行浮点数的运算的呢？我们已经知道，浮点数在CPU中是通过指数的形式表示的，以加法为例，我们是如何对浮点数进行运算的？如两个数a = 1.23*10³和 b = 4.25*10⁸，我们有一种比较快捷的办法：
a = 1.23*10³
b = 425000*10³
a + b = 42501.23*10³

对于计算机来说，这个办法尤其简单，当把指数移位成相同之后，两个浮点数的加减乘除都变得很容易了，浮点数的加减法的运算一般分为:0操作数的检查，比较阶码大小并完成对阶，尾数进行加减运算，结果规格化并进行舍入处理。具体的流程推荐查看这篇文章。
所以，我们说的浮点数运算就可能在两个地方损失精度，第一是十进制转化二进制的时候，由于浮点数长度限制，可能会出现尾数被舍弃的情况，第二是在浮点运算对阶的时候，会对尾数进行移位操作，也可能会损失部分精度，第三是尾数相加保存的时候，可能也会有丢弃某一位的情况。那么0.1+0.2是在哪里出了问题，我们来还原一下现场。
第一步，对0.1和0.2分别求出其二进制表示形式:
(0.1)₁₀=(0.0001100110011001100110011…)₂=1.10011001100110011001101*2^-4（偶数优先舍入原则+1）
(0.2)₁₀=(0.0011001100110011001100110…)₂=1.10011001100110011001101*2^-3（偶数优先舍入原则+1）
指数相差1，对较小数字a进行对阶，并对尾数相加:
a = 0.11001100110011001100110*2^-3（偶数优先舍入原则-1）
b = 1.10011001100110011001101*2^-3
a + b = 10.01100110011001100110011*^-3
a + b = 1.00110
011001100110011010*^-2（偶数优先舍入原则+1）
此时a+b用二进制表示则为0-01111101-00110011001100110011010，用16进制表示则为0x3e99999a，转换成十进制等于0.30000001192092896000。

但是这里有一个问题，我用javascript，python，c语言分别测试，发现javascript和python环境下0.1+0.2等于0.30000000000000004，而c语言是等于上述的结果，希望能有高手指出来这是什么原因。

参考资料

1. IEEE754
2. 浮点运算
3. 浮点数的运算原理–IEEE 754
4. 浮点数解惑